r-PPG Review
Algorithm available for r-PPG (based on referenced articles)
Skin Reflection model 1
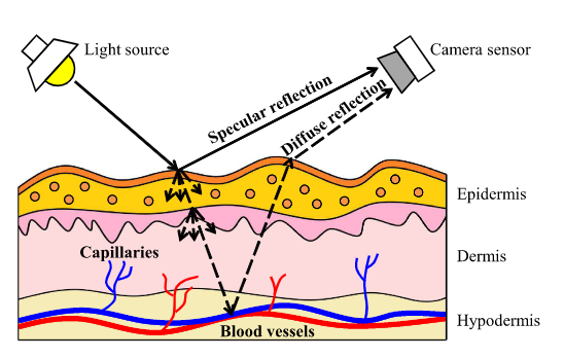
The reflection of each skin pixel in a recorded image sequence can be defined as a time-varying function in RGB channels $$\textbf{C}_k(t)=I(t)\cdot(\textbf{v}_s(t)+\textbf{v}_d(t))+\textbf{v}_n(t)$$ where
- $\textbf{C}_k$: RGB channels of the $k$th skin pixel
- $I(t)$: Luminance intensity level
- $\textbf{v}_s(t)$: specular reflection
- $\textbf{v}_d(t)$: diffusion reflection
- $\textbf{v}_n(t)$: noise
Specular reflection: $$\textbf{v}_s(t)=\textbf{u}_s\cdot(s_0+s(t))$$ where
- $\textbf{u}_s$: unit color vector of the light spectrum
- $\textbf{s}_0+s(t)$: stationary and varying parts of specular reflections ($s(t)$ is induced by motion)
Diffusion reflection: $$\textbf{v}_d(t)=\textbf{u}_d\cdot d_0+\textbf{u}_p\cdot p(t)$$ where
- $\textbf{u}_d$: unit color vector of the skin tissue
- $d_0$: stationary reflection strength
- $\textbf{u}_p$: relative pulsatile strengths in RGB channels
- $p(t)$: pulse signal
Combine the formula above $$\textbf{C}_k(t)=I(t)\cdot(\textbf{u}_s\cdot(s_0+s(t))+\textbf{u}_d\cdot d_0+\textbf{u}_p\cdot p(t)))+\textbf{v}_n(t)$$ then combine $\textbf{u}_s\cdot s_0 +\textbf{u}_d\cdot d_0$ into $\textbf{u}_c\cdot c_0$ and transform $I(t)$ into a startionary part $I_0$ and a time-varying part $I_0\cdot i(t)$ $$\textbf{C}_k(t)=I_0\cdot(1+i(t))\cdot(\textbf{u}_c\cdot c_0+\textbf{u}_s\cdot s(t)+\textbf{u}_p\cdot p(t)))+\textbf{v}_n(t)$$
we assume that a sufficiently high number of pixels are focused on comparable skin tissues and the averate of $\textbf{C}_k$ can be denoted as $$C(t)\approx I_0\cdot(1+i(t))\cdot(\textbf{u}_c\cdot c_0+\textbf{u}_s\cdot s(t)+ \textbf{u}_p\cdot p(t))$$ after expansion and simplification, the formula becomes $$\textbf{C}(t)\approx\textbf{u}_c\cdot I_0\cdot c_0+\textbf{u}_c\cdot I_0\cdot i(t)+\textbf{u}_s\cdot I_0\cdot s(t)+\textbf{u}_p\cdot I_0\cdot p(t)$$
rPPG Methods (without Deep Learning)
BSS-Based Methods(PCA2/ICA3)
- BSS: Blind source spearation
- PCA: Principal Component Analysis
- ICA: Independent Component Analysis
$$\textbf{Y}(t)=\textbf{W}\cdot \textbf{C}(t)$$
- $\textbf{Y}(t)$: factorized source signals consisting of pulse and noise
- $\textbf{W}$: demixing matrix (estimated by PCA or ICA)
Principle: Select the most periodic signal from $\textbf{Y}(t)$ as the pulse Shortage: Cannot deal with the cases of periodic motion.
limitations for estimation:
- PCA: Covariance of RGB signals (ie., eigenvectors)
- ICA: Assuming components in $\textbf{Y}(t)$ are statistically independent and non-gaussian, requires $\textbf{C}(t)$ long enough for statistical measurement.
Model-Based Methods
Demixing signal based on knowledge of the color vectors
Define normalization matrix $\textbf{N}$ makes $\textbf{N}\cdot \overline{\textbf{C}(t)}=\textbf{N}\cdot \textbf{u}_C\cdot I_0\cdot c_0=\textbf{1}$
where $\textbf{N}$ is used to temporally normalize $\textbf{C}(t)$ as $$\textbf{C}_n(t)=\textbf{N}\cdot\textbf{C}(t)=\overbrace{\textbf{1}\cdot(1+i(t))}^{\text{Intensity}}+\overbrace{\textbf{N}\cdot\textbf{u}_s\cdot I_0\cdot s(t)}^\text{Specular}+\overbrace{\textbf{N}\cdot\textbf{u}_p\cdot I_0\cdot p(t)}^\text{Pulse}$$ where
- Intensity: light intensity variations. Usually the largest component in $\textbf{C}_n(t)$ due to motion-induced intensity variation.
- Specular: Temporal variations along the direction of the scaled specular reflection.
- Pulse: Pulse-induced temporal color variations. Depends on the luminance spectrum and camera sensor.
Model-based methods use DC-Removed signal for pulse extraction: $$\tilde{\textbf{C}}_n(t)=\textbf{C}_n(t)-\textbf{1}$$
PBV4
Projecting $\tilde{\textbf{C}}_n(t)$ onto a single direction $\textbf{z}$ to create an estimate $\hat{p}(t)$ that is proportional to $p(t)$. $$\hat{p}(t)=\tilde{\textbf{C}}_n^\top(t)\cdot\textbf{z}=k\cdot p(t)$$ Assume $p(t)$ is uncorrelated with the other signal sources $$\textbf{E}[p(t)\cdot i(t)]=\textbf{E}[p(t)\cdot s(t)]=0$$ $$\textbf{E}[\tilde{\textbf{C}}_n(t)\cdot\hat{p}(t)]=\textbf{E}[\tilde{\textbf{C}}_n(t)\cdot\tilde{\textbf{C}}_n^\top(t)]\cdot\textbf{z}=k\cdot\textbf{E}[\tilde{\textbf{C}}_n(t)\cdot p(t)]\approx k\cdot \textbf{N}\cdot\textbf{u}p\cdot I_0\cdot\textbf{E}[p(t)\cdot p(t)]$$ PBV algorithm assumes a prior-known blood volume pulse vector $\textbf{u}{\text{pbv}}=\textbf{N}\cdot\textbf{u}_p\cdot I_0$
Reference
- [1] Wang, Wenjin, et al. “Algorithmic principles of remote PPG.” IEEE Transactions on Biomedical Engineering 64.7 (2016): 1479-1491.
- [2] Lewandowska, Magdalena, et al. “Measuring pulse rate with a webcam—a non-contact method for evaluating cardiac activity.” 2011 federated conference on computer science and information systems (FedCSIS). IEEE, 2011.
- [3] Poh, Ming-Zher, Daniel J. McDuff, and Rosalind W. Picard. “Advancements in noncontact, multiparameter physiological measurements using a webcam.” IEEE transactions on biomedical engineering 58.1 (2010): 7-11.
- [4] De Haan, Gerard, and Arno Van Leest. “Improved motion robustness of remote-PPG by using the blood volume pulse signature.” Physiological measurement 35.9 (2014): 1913.
- [5] De Haan, Gerard, and Vincent Jeanne. “Robust pulse rate from chrominance-based rPPG.” IEEE Transactions on Biomedical Engineering 60.10 (2013): 2878-2886.
